Randomization Methods – ARCHIVED

CHAPTER SECTIONS

Experimental Designs and Randomization Schemes


Section 4

Randomization Methods – ARCHIVED

Contributors

As with individually randomized trials, a number of considerations need to be addressed up front for CRTs to avoid downstream problems. In particular, potential confounding is always an issue. For example, if elderly patients are more likely than younger patients to acquire nosocomial infections, it would be important to ensure that one of the arms of the trial is not more likely to consist of elderly patients. In this example, if the clusters are hospital wards, there should be some assurance of balance in the average ages of the wards assigned to one arm compared to the other. Sometimes there are several potential confounders that might play a role.

As with individually randomized trials, a number of considerations need to be addressed up front for CRTs to avoid downstream problems. In particular, potential confounding is always an issue. For example, if elderly patients are more likely than younger patients to acquire nosocomial infections, it would be important to ensure that one of the arms of the trial is not more likely to consist of elderly patients. In this example, if the clusters are hospital wards, there should be some assurance of balance in the average ages of the wards assigned to one arm compared to the other. Sometimes there are several potential confounders that might play a role.

Stepped-Wedge Designs

When a PCT employs cluster randomization, the simplest approach is parallel randomization, in which clusters are randomly assigned to the intervention or control condition throughout the trial with no crossover. In some studies, preparing all of the intervention clusters to start the intervention at the same time may not be feasible. The stepped-wedge CRT design overcomes this problem by gradually introducing the intervention to groups of clusters over time. Clusters are divided into several groups, usually 4 to 6, and all clusters start the trial in the control condition. Groups of clusters cross over to the intervention condition in random order and on a staggered schedule, and all groups receive the intervention before the end of the trial (see figure below). The stepped-wedge design also has the benefit of allowing researchers to record and incorporate into the analyses changes to the hospital or health system that happen over time and have the potential to affect the study (Cook et al 2016).

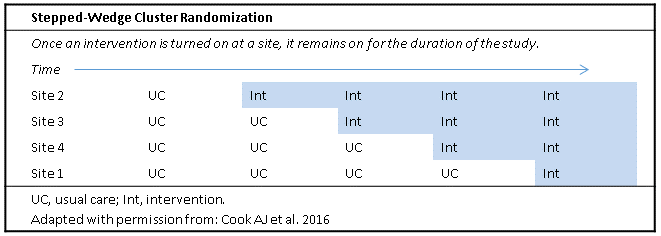
Stepped-Wedge Cluster Randomization Example

Because all sites eventually will receive the intervention, a stepped-wedge trial may be more appealing to the broader community and thus lead to more robust study participation, especially in cases where the intervention seems particularly promising (Hussey and Hughes 2007).

Case Example: The LIRE Study

The Pragmatic Trial of Lumbar Image Reporting with Epidemiology (LIRE), an NIH Collaboratory Trial, is testing an intervention that inserts epidemiologic benchmarks into reports from lumbar spine imaging. LIRE will seek to determine whether this simple informational intervention can reduce subsequent testing and treatments that may not provide any benefit to patients. LIRE is an example of a stepped-wedge CRT (Jarvik JG et al 2015). Clinics in 4 large healthcare systems are randomized to initiate the intervention as part of 1 of 5 "waves" corresponding to prespecified calendar dates.

Pair Matching and Stratification With Cluster Designs

Two popular mechanisms for achieving balance are pair matching and stratification. With pair matching, clusters are paired in terms of their potential confounders and then within each pair, one cluster is randomized to receive one of the arms and the other cluster receives the opposite arm. For example, considering age and sex as potential confounders, clusters would be matched into pairs such that the average age and the percent female are approximately equal. Likewise, the sizes of the 2 clusters should be similar. Stratification is a generalization of pair matching in that strata are formed based on the potential confounders; within each stratum, a randomization scheme that ensures balance is developed. For example, if there are 11 clusters in one stratum, the randomization would assign 5 clusters to one arm and 6 to the other. However, when there are several confounders, it can be difficult to use stratification or pair matching.

Constrained Randomization

Another method that is increasingly being studied and implemented for CRTs is constrained randomization (Li et al 2016). Exploiting the fact that all of the clusters are identified before randomization, they can each be characterized in terms of the levels of several potential confounders. For any possible randomization of this set of clusters, a balance metric (several exist) is applied to “measure” the amount of imbalance that would exist if that particular randomization were applied. It is possible to generate a large number of potential randomization schemes; in fact, with very few clusters, every possible randomization scheme can be tabulated in this way, along with their respective balance scores. By some predefined criterion, such as a certain percentage of all possible randomizations, a set of clusters with the least amount of imbalance is chosen as the “randomization space.” From this “randomization space,” a single randomization scheme is selected. There are many statistical issues that are still being explored with respect to this strategy.

For additional information about considerations affecting study design decisions, see also Designing With Implementation and Dissemination in Mind.

Previous Section Next Section

SECTIONS

CHAPTER SECTIONS

sections

  1. Introduction – ARCHIVED
  2. Statistical Design Considerations – ARCHIVED
  3. Cluster Randomized Trials – ARCHIVED
  4. Randomization Methods – ARCHIVED
  5. Choosing Between Cluster and Individual Randomization – ARCHIVED
  6. Alternative Cluster Randomized Designs – ARCHIVED
  7. Concealment and Blinding – ARCHIVED
  8. Designing to Avoid Identification Bias – ARCHIVED
  9. Additional Resources – ARCHIVED

Resources

Pragmatic and Group-Randomized Trials in Public Health and Medicine—Part 3. Analysis Approaches
Online course From the NIH Office of Disease Prevention

Pair-Matching vs Stratification in Cluster-Randomized Trials
Guidance document from the Biostatistics and Study Design Core

Advanced Methods for Primary Care Research: The Stepped Wedge Design
Presentation from the Agency for Healthcare Research and Quality providing a technical overview of applications of the stepped-wedge design in clinical research

REFERENCES

back to top

Cook AJ, Delong E, Murray DM, Vollmer WM, Heagerty PJ. 2016. Statistical lessons learned for designing cluster randomized pragmatic clinical trials from the NIH Health Care Systems Collaboratory Biostatistics and Design Core. Clin Trials. 13:504-512. doi:10.1177/1740774516646578. PMID: 27179253.

Li F, Lokhnygina Y, Murray DM, Heagerty PJ, DeLong ER. 2016. An evaluation of constrained randomization for the design and analysis of group-randomized trials. Stat Med. 35:1565-1579. doi:10.1002/sim.6813. PMID: 26598212.

back to top

Jarvik JG, Comstock BA, James KT, et al. 2015. Lumbar Imaging With Reporting Of Epidemiology (LIRE)--Protocol for a pragmatic cluster randomized trial. Contemp Clin Trials. 45(Pt B):157-163. doi:10.1016/j.cct.2015.10.003. PMID: 26493088.

Hussey MA, Hughes JP. Design and analysis of stepped wedge cluster randomized trials. 2007. Contemp Clin Trials. 28:182-191. doi:10.1016/j.cct.2006.05.007. PMID: 16829207.


Version History

July 7, 2020: Moved down the LIRE case example (changes made by D. Seils).

July 2, 2020: Minor corrections to layout and formatting (changes made by D. Seils).

May 27, 2020: Revised and moved up the Stepped-Wedge Designs subsection, added the “Part 3. Analysis Approaches” online tutorial to the Resources sidebar, added Heagerty to the contributors list, and reordered the sections of this chapter as part the annual content update (changes made by D. Seils).

January 16, 2019: Updated the introduction and the description of stepped-wedge designs, embedded a video on randomization methods, and made nonsubstantive changes to the text as part of the annual content update (changes made by D. Seils).

Published August 25, 2017

current section :

Randomization Methods – ARCHIVED

  1. Introduction – ARCHIVED
  2. Statistical Design Considerations – ARCHIVED
  3. Cluster Randomized Trials – ARCHIVED
  4. Randomization Methods – ARCHIVED
  5. Choosing Between Cluster and Individual Randomization – ARCHIVED
  6. Alternative Cluster Randomized Designs – ARCHIVED
  7. Concealment and Blinding – ARCHIVED
  8. Designing to Avoid Identification Bias – ARCHIVED
  9. Additional Resources – ARCHIVED

Citation:

Heagerty PJ, DeLong ER; for the NIH Health Care Systems Research Collaboratory Biostatistics and Study Design Core. Experimental Designs and Randomization Schemes: Randomization Methods – ARCHIVED. In: Rethinking Clinical Trials: A Living Textbook of Pragmatic Clinical Trials. Bethesda, MD: NIH Pragmatic Trials Collaboratory. Available at: https://rethinkingclinicaltrials.org/chapters/design/experimental-designs-randomization-schemes-top/randomization-methods/. Updated July 9, 2025. DOI: 10.28929/007.